Problem Statement
Given a 2D board and a list of words from the dictionary, find all words in the board.
Each word must be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Note:
- All inputs are consist of lowercase letters a-z.
- The values of words are distinct.
Example
Input:
board = [
['o','a','a','n'],
['e','t','a','e'],
['i','h','k','r'],
['i','f','l','v']
]
words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]
Explanation
This problem builds on Word Search, the only difference being instead of searching for one particular word, we are now given a set of words. We could take our solution from the Word Search problem and run that algorithm for every word in the data set which would result in a lot of wasted computations as the nested for loops which iterate the board looking for a matching first character will have to run for every word in the word list.
There could be a better solution using a Trie. A Trie from the word reTRIEval is a solid data structure for string matching problems. We will be using a Prefix Trie in particular.
A trie for the following dataset [oat, oath, eat, lie, lick] would look like:
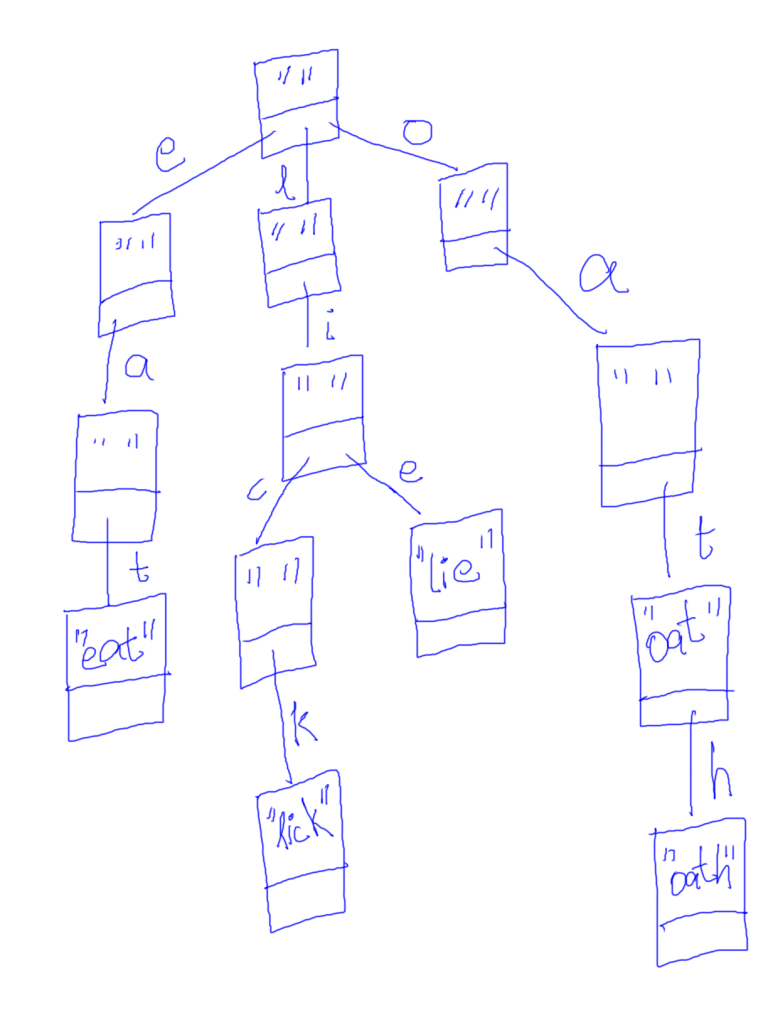
Note: The root node of a Trie always stores null as it’s data.
The code to represent a Trie would be like:
class TrieNode {
var children = [Character:TrieNode]()
var word: String?
subscript(child: Character) -> TrieNode? {
get {
return children[child]
}
set {
children[child] = newValue
}
}
}
A lot of examples online use an array to represent the children of the TrieNode. The length of the array is assumed to be the length of the alphabet that is being represented. For English, the length would be 26 assuming we stick to either upper case or lower case. If you want to mix the two then it becomes 52. In my opinion this is limiting us and we can easily get by this limitation by using a map of [Character:TrieNode]. This enables us to build a Trie with English, Chinese, Japanese, French and even with Emoji characters!
The routine to build the Trie is pretty straight forward:
func generateTrie(words: [String]) -> TrieNode {
let root = TrieNode()
for word in words {
var temp = root
for (i,c) in word.enumerated() {
if temp[c] == nil {
temp[c] = TrieNode()
}
if i == word.count - 1 {
temp[c]?.word = word
}
temp = temp[c]!
}
}
return root
}
We simply iterate through the list of words, extract each character from the word and add it as a child of the previous node.
Assuming the length of the biggest word is L and we have N such words in our data set, the time and space complexity for setting up and storing the Trie would be O(LN).
So how does the Trie help us? To begin with looking up if a character succeeds a character is a constant time operation in a Trie.
So how does this algorithm work? The i and j for loops in the findWords(::) function will iterate through the board and at each iteration, will check if the root of the Trie has a reference to the character at that position in the board. If yes, it will mark the current alphabet as visited and call the dfs(i: j: node: map inout: board: result inout) function starting at indices i and j. When this call returns, we update the visited value for these indices.
The code is as follows:
func dfs(i: Int, j: Int, node: TrieNode, map:inout [[Bool]], board:[[Character]], results: inout Set<String>) {
let topRow = i - 1
let bottomRow = i + 1
let leftColumn = j - 1
let rightColumn = j + 1
let numRows = board.count
let numCols = board[0].count
if let word = node.word {
results.insert(word)
}
if topRow >= 0 && !map[topRow][j] && node[board[topRow][j]] != nil {
map[topRow][j] = true
dfs(i: topRow, j: j, node: node[board[topRow][j]]!, map: &map, board: board, results: &results)
map[topRow][j] = false
}
if bottomRow < numRows && !map[bottomRow][j] && node[board[bottomRow][j]] != nil {
map[bottomRow][j] = true
dfs(i: bottomRow, j: j, node: node[board[bottomRow][j]]!, map: &map, board: board, results: &results)
map[bottomRow][j] = false
}
if leftColumn >= 0 && !map[i][leftColumn] && node[board[i][leftColumn]] != nil {
map[i][leftColumn] = true
dfs(i: i, j: leftColumn, node: node[board[i][leftColumn]]!, map: &map, board: board, results: &results)
map[i][leftColumn] = false
}
if rightColumn < numCols && !map[i][rightColumn] && node[board[i][rightColumn]] != nil {
map[i][rightColumn] = true
dfs(i: i, j: rightColumn, node: node[board[i][rightColumn]]!, map: &map, board: board, results: &results)
map[i][rightColumn] = false
}
}
func findWords(_ board: [[Character]], _ words: [String]) -> [String] {
if board.isEmpty || words.isEmpty {
return [String]()
}
var results = Set<String>()
let root = generateTrie(words: words)
var map = board.map { (row) -> [Bool] in
row.map({ (c) -> Bool in
return false
})
}
let numRows = board.count
let numCols = board[0].count
for i in stride(from: 0, to: numRows, by: 1) {
for j in stride(from: 0, to: numCols, by: 1) {
if root[board[i][j]] != nil {
map[i][j] = true
dfs(i: i, j: j, node: root[board[i][j]]!, map: &map, board: board, results: &results)
map[i][j] = false
}
}
}
return Array(results).sorted()
}
Time Complexity
The time complexity of the i and j for loops is O(RC) in terms of number of rows and columns in the board. The call to perform DFS is done every time an encountered character from the board is found to be a child of the root Trie node and DFS is recursively called based on the length of the word and if we have N words of size L, the recursion will take O(LN). It really comes down to a situation if RC >> LN then O(RC) is the dominating factor and vice versa.
Space Complexity
There’s O(LN) additional space needed for setting up the Trie.
The problem is taken from Leetcode.
Solution is hosted on Github.